The Beginner's Guide to LUTs

Colour, colour everywhere...

Replay: Phil Rhodes provides everything you always wanted to know about LUTs...

Making pictures look subtly different – or even drastically different – is something that's been commonplace for years in post production. Sneaking up on over the last ten years or so has been the requirement to juggle grading and calibration on set, too, and as with anything that touches the picture, there's a mesmerising variety of ways to make horrible mistakes.

Purpose and Application

It's the object of this piece to avoid that problem, of course, and the best place to start is with a thorough understanding of lookup tables, what they're for, and how they're implemented, as well as how they relate to alternative approaches such as numerically-defined transforms. Lookup tables, or LUTs, are used everywhere, from cameras, conversion devices and monitors to post production software and even command line processing tools.

Regardless of the circumstances, though, the purpose of a lookup table is to make colour and brightness adjustments to a picture, whether that's a picture in a file on a workstation or one flying down a cable. The reasons for doing this are varied. A box designed to apply a calibration to a display (or a built-in feature in a display which performs the same function) is using a LUT. Loading a LUT into a camera might be intended to apply creative colour and brightness changes to the camera's monitoring output, so as to approximate the look of the final production for the benefit of people on set while retaining the option to tweak in post. In other circumstances, a LUT might be applied to image data that isn't designed to be directly viewed – such as a log output from a camera – in order to make it easier to look at.

In practice, LUTs are generally handed around as files, and there are, unfortunately, a lot of incompatible formats and sometimes no loss-free way to convert between them. Creating a grade on some test footage, then taking that grade on set in a monitor or camera, is a completely reasonable desire, but there can be a few stumbling blocks in the way.

Principal Types of LUT

There are three main technical approaches to altering brightness and colour in images: one-dimensional LUTs, three-dimensional LUTs, and, as a side issue, mathematical transformations. There is, for reasons that should soon be clear, no such thing as a 2D LUT. In general, though, the term “lookup table” can be taken fairly literally: for each input value there's a fixed output value.

One-dimensional LUTs are perhaps most comparable to something like Photoshop's curves filter, where each of the red, green and blue colour channels is treated separately – possibly they're better described as a set of three lists of values. Often, 1D LUTs work in ten bits, so for each RGB channel there are 1024 values and the operation is very literal. Let's consider an example lookup table, which only has 10 values, to keep things straightforward.

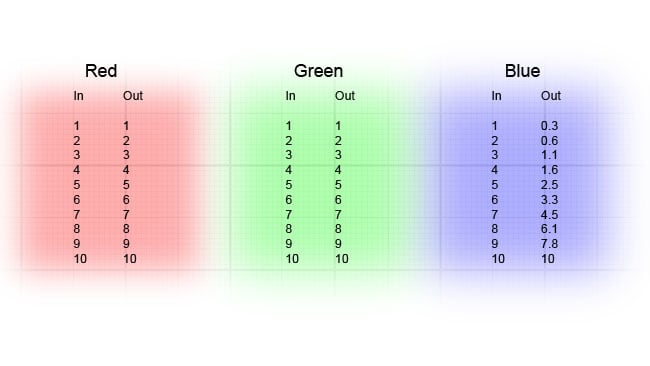
Fig. 1: The three numerical lists of a 1D LUT

As we can see, most of the numbers in the red and green channels simply increment one by one, row by row; the output, in these cases, will be the same as the input. The blue channel, however, contains numbers that don't always increment by one. Let's draw a quick chart of the values, so we can get a good idea what they might do:

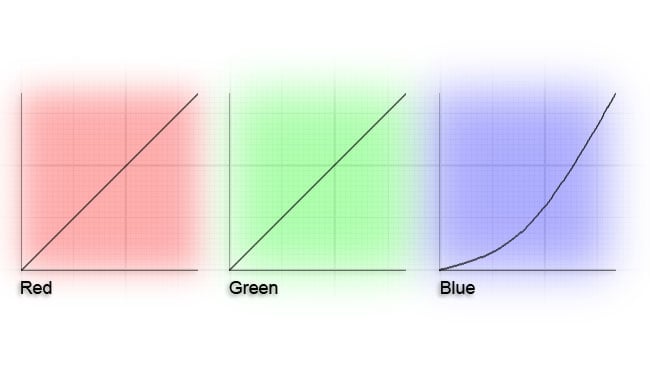
Fig. 2: The curves described by the example LUT

As we can see, the blue channel has been reduced in its midtones – a reduction in blue gamma. This has the effect of pushing the image toward yellow. It will do this to more or less anything, although the look of the effect can be quite dependent on the picture content.

Fig. 3: 1D LUT on image

This illustrates one of the key issues with LUTs, particularly those intended to change an image that's in one standard – say Sony's SLog3 low-contrast curve – into another, such as the monitoring standard ITU-T Recommendation 709 (Rec. 709). A one-dimensional lookup table can do this. What a 1D LUT can't do, however, is to change something that's entirely blue into something that's entirely red, or alter the appearance of, say, pinkish-purple objects without altering anything else. A 1D LUT is very much the equivalent of the “curves” filter from Photoshop – and in fact, that filter can actually save lookup tables which can, by various means, be converted into formats suitable for use in other software and hardware devices. Click the pen icon, click the poorly-designed button to the right of the “preset” dropdown, and hit “save”. The resulting .amp file is a basic 1D LUT; software such as Resolve has the ability to output more complicated things. Note that if you don't get an .amp file, it isn't a conventional LUT; click the pen icon and try again.

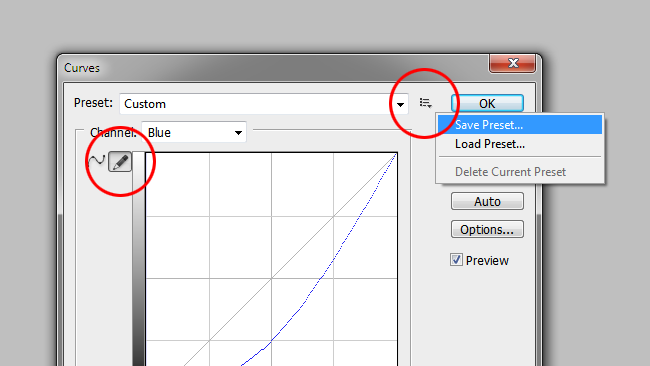
Fig. 4: Saving a LUT from Photoshop's Curves filter

So, if something contains a lot of blue, a 1D LUT can reduce that amount, but there's no way to tie the amount of blue to the amount of red or green. In an artistic sense, if we're trying to implement a grade, a 1D LUT can't, for instance, do a hue rotation, or reduce or increase saturation.

3D Lookup Tables

We can get around the limitations of 1D LUTs with 3D LUTs, which are a little bit more complicated than just lists of numbers. Instead of concentrating on individual RGB colour channels, each in isolation, a 3D LUT considers the complete set of three RGB values – a triplet - for each pixel. Sometimes this is visualised, and referred to, as a cube (.cube is one of the common file formats for 3D LUTs).

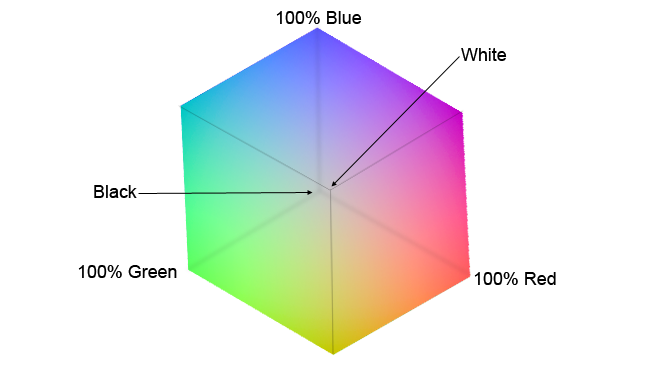
Fig. 4A – Colour visualised as a cube

If we nominate one of the corners of the cube as RGB zero, or black, we can imagine the red, green and blue input values as representing distances along the three edges of the cube that meet at that corner. By measuring the appropriate distances along the edges of the cube, we can designate a point inside it. At that location is another set of three numbers representing the output value.

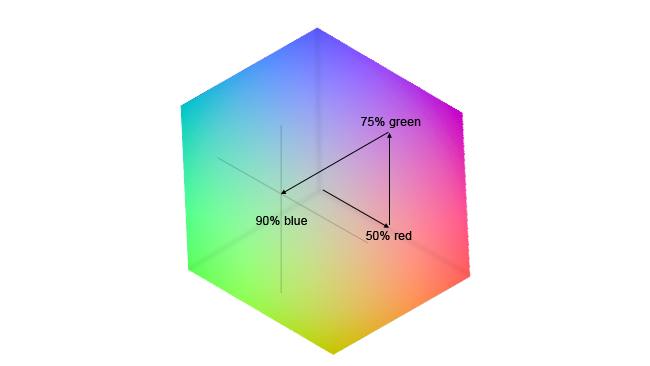
Fig. 5 – The input value shown here is 50% red, 75% green and 90% blue (RGB 128, 192, 230 in 8-bit colour). The output value could be anything.

This works really well; any possible colour can be translated into any other colour. The problem is simply one of scale. Real digital cinematography applications need 3D LUTs that have at least 1024 entries on each edge. For a simple 1D lookup table with 10-bit precision, we need to store just three sets of 1024 numbers, for a total of 3072 numbers, each ten bits long. That's just a few kilobytes of storage space – less than most emails. But for a 3D LUT, to store a corresponding output value for every possible colour in a ten-bit image, is hugely more data. There are 1024 * 1024 * 1024 total colours in a ten-bit image, or just over a billion, meaning that a lookup table representing a specific 10-bit RGB output value for every input value would be nearly 4GB in size – and that's just for 10-bit data. That's large to the point of being difficult to store and transport, at least casually in email attachments and the like.

So real 3D LUTs – real cubes – don't store one explicit output value for every input value. There isn't a number at every single point within the cube. Instead, they store a lower-resolution scattering of numbers – so any given input value might appear inbetween the available output values.

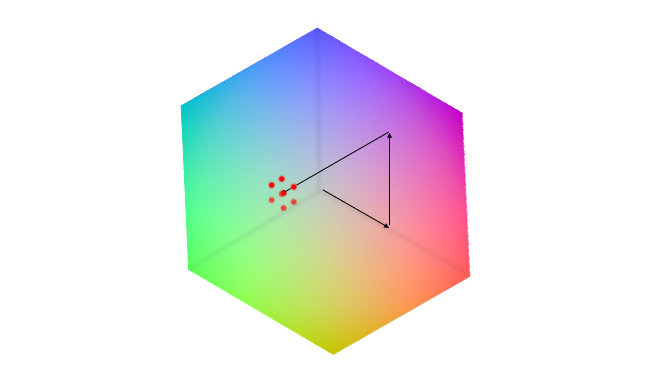
Fig. 6 – The desired output value lies between several of the values given in a low-resolution 3D LUT (the red spots) 

The problem is that when a number is looked up, it must be interpolated from the nearest available values, and the interpolation is not perfect. Whatever technique was used to create the original lookup table, there's no guarantee that the interpolated value will be identical. It should be close, but it won't be exactly the same set of numbers, and the interpolation can often be quite basic as it must be performed around two million times per HD frame. Often, this works out OK, but if the LUT contains any particularly adventurous colour adjustments, as it might if it represented a particularly extreme creative grade, it can become possible to see banding or quantisation noise in what should be smooth gradients of colour.

And the requirements here can be quite significant. Some cubes are stored at a resolution of only 17 by 17 by 17 entries, meaning that each set of numbers given in the stored LUT influences a range of RGB numbers in a 10-bit image that's more than 60 values wide. This is generally something that improves with sticker price – lower-cost LUT processing boxes might only accept 17-cubed-entry LUTs. Paying more might yield a device capable of taking 64-cubed-entry LUTs, reducing the visibility of this sort of error.

A word on mathematical colour adjustments

When a piece of software performs a colour adjustment on an image, it doesn't generally use lookup tables (though some do, occasionally, as an internal shortcut). Instead, the required colour change is worked out as a piece of mathematics. The term “gamma” itself comes from the name of a term in a mathematical equation. Lift, gamma and gain are the traditional adjustments in video amplifiers and telecine transfer suites and they can all be modelled mathematically; that's what the ASC's Color Decision List (CDL) does. It specifies lift, gamma and gain terms for each of the RGB channels, and an overall saturation adjustment.

Fig. 7 – Output image has 0.25 blue lift, red gamma of 1.2 and green gain of 1.25, producing a smoky, faded look.

It's simplistic, suffering at least some of the problems of a 1D LUT , give or take the saturation option. Either way, it is intended to be a widely portable way of expressing basic colour correction intentions, and is rather simpler to implement than a 3D LUT. Crucially, mathematical adjustments like this don't suffer the issues of precision and quantisation noise associated with some 3D LUTs, but the difference in capabilities means that the two concepts aren't directly equivalent.

Limitations, Applications and Requirements

Applications for lookup tables in general range from standards conversion to artistic license, but in either case the intent is the same: so that the image we see is as similar as possible to the final result. That's fairly obvious, though; the question is why it can be such a big deal. After all, we never have anything even remotely approaching accurate representation of what 35mm film will look like in the end.

The thing is, everyone understands that. Nobody makes judgements about the on-set images from a 35mm video tap, because everyone knows they're completely inaccurate. If a monitor is going to be right, though, it needs to be very close to right – both to ensure we know what we're shooting, and so that everyone's expecting the same results. Or, of course, it's also quite possible to make up a 3D LUT that produces a black-and-white, high-contrast image, and tell everyone it's a video tap.